Translate this page into:
Evaluation of the Effects of the Dental and Skeletal Anchored Face Mask Therapies on the Craniofacial System by Using Nonlinear Finite Element Analysis
Address for correspondence: Dr. Beril Demir Karamanli, Istanbul University, Faculty of Dentistry, Department of Orthodontics, 34093, Capa-Fatih, Istanbul, Turkey. E-mail: berilkaramanli@gmail.com
This article was originally published by Wolters Kluwer and was migrated to Scientific Scholar after the change of Publisher.
Abstract
Aims
The aim of this study was to evaluate the biomechanical effects on the craniofacial complex of skeletal anchorage and dental anchorage during face mask therapy.
Subjects and Methods
Two nonlinear finite element (FE) simulations were performed using a three-dimensional FE model. Face mask therapy with dental anchorage in the upper canines and face mask therapy with skeletal anchorage in the piriform apertures of the maxilla were simulated. In both simulations, the magnitude of the applied force was 750 g per side, and the force direction was 30° forward and downward relative to the occlusal plane.
Results
The circummaxillary sutures showed greater and more uniform stresses in the skeletal anchorage model than the dental anchorage model. This is the result of the more parallel forward movement of the maxilla in the skeletal anchorage model.
Conclusions
In Class III malocclusions with maxillary deficiency, for improved effects on the maxilla, choosing skeletal anchorage may be more effective in face mask therapies
Keywords
Craniofacial system
face mask
finite element analysis
skeletal anchorage
Introduction
For many years, Class III malocclusion with maxillary deficiency has been treated by protraction of the maxilla with an orthopedic face mask which is anchored from maxillary teeth. Some investigations have demonstrated the skeletal and dentoalveolar effects of this conventional dental anchored appliance in a short-term treatment including forward displacement of the maxilla, counterclockwise rotation of the maxilla depending on the force application point, clockwise rotation of the mandible, protrusion of the maxillary incisors, and retrusion of the mandibular incisors.[1-4] However, the skeletal effects of this conventional appliance are still controversial.[5] In some long-term follow-ups, there were no significant between-group differences in skeletal changes compared to control group.[6,7]
To improve the skeletal effects, osseointegrated implants, orthodontic miniscrews, and miniplates have been substituted for conventional dental anchorage and used as skeletal anchorage in maxillary protraction. Several studies have demonstrated the dramatic skeletal effects of maxillary protraction using skeletal anchorage.[8-12]
In face mask therapies, retraction forces are applied on the mandible by the chin part of the face mask appliance, along with the protraction force applied on the maxilla. In all of the previous studies, only maxillary protraction was simulated and effects of the mandibular protraction force, which is known to be 70%–75% of the magnitude of the protraction force applied on the maxilla,[13] was ignored. It might be helpful to evaluate the effects of the face mask therapy not only as maxillary protraction but also as mandibulary retraction.
The aim of this study was to use the finite element (FE) method to investigate and compare the stress distributions in the craniofacial complex including the mandible and temporomandibular joint (TMJ), both when teeth and bone were used as anchorage for face mask application.
Subjects and Methods
The three-dimensional (3D) structural analysis of the craniofacial complex was performed under the conditions which are dental anchorage and skeletal anchorage using the 3D FE method. 3D model of the craniofacial complex obtained by 3D optic scanning of the real craniofacial bones of an adolescent skull was supplied from a company (21st Century Solutions Ltd., Suite 31, Don House, 30–38 Main Street, Gibraltar). The 3D model was saved as digital imaging and communications in medicine file and then imported to CATIA V5 R14 (Dassault Systèmes) software for the preparation of the 3D model. TMJ discs and circummaxillary sutures were constructed in CATIA V5 environment. The reconstructed geometry of craniofacial complex was exported in STL file format. The STL file was imported into SAMCEF Field (SAMTECH), which was used to perform the 3D FE analysis having the processing steps as following; finalizing the 3D geometry, creating the volume mesh from the 3D geometry of the craniomaxillary complex, assigning the boundary conditions and the material properties, introducing the loads, running the analysis, and performing postprocessing. The 3D model of the craniomaxillary complex was meshed with 539,262 tetrahedral elements of which have totally 135,823 nodes. The material properties of the bones, teeth, sutures, and TMJ discs were defined according to experimental data from previous studies[14,15] [Table 1]. The materials of the TMJ discs and sutures were assumed as viscoelastic which made the analysis nonlinear. Regarding the modeling of the viscoelastic material, the Kelvin model was used.[16]
| Young modulus (MPa) | Poisson ratio (v) | |
|---|---|---|
| Cortical bone | 13,700 | 0.3 |
| Teeth | 20,290 | 0.3 |
| Cartilage layers | 0.79 | 0.49 |
In the first simulation of the face mask application using a dental anchorage, a 750 g force directed from the upper canines was applied to per side forward and 30° downward relative to the occlusal plane. In the second simulation of face mask therapy with skeletal anchorage, the force was applied as 750 g directed from the aperture priform region to the per side forward and 30° downward relative to the occlusal plane.
When the maxillary protraction force was applied on the maxilla, the generated force on the mandible was simulated as 1000 g in the direction of chin-condyle head and retraction force in 500 g was generated on the forehead as the moments were calculated. The duration of the analysis is determined as 300 s.
Results
In dental anchored face mask simulation; high von Mises stress values were seen in condyle necks (0.85 MPa), forehead (0.65 MPa), frontal process of maxilla (0.55 MPa), frontal edge of nasal bone (0.41 MPa), frontomaxillary suture (0.34 MPa), zygomatic bone (0.30 MPa), TMJ disc (0.12 MPa), nasomaxillary suture (0.11 MPa), zygomaticotemporal suture (0.09 MPa), pterygopalatine suture (0.03 MPa), and zygomaticomaxillary suture (0.01 MPa) in descending order [Figure 1a-j].
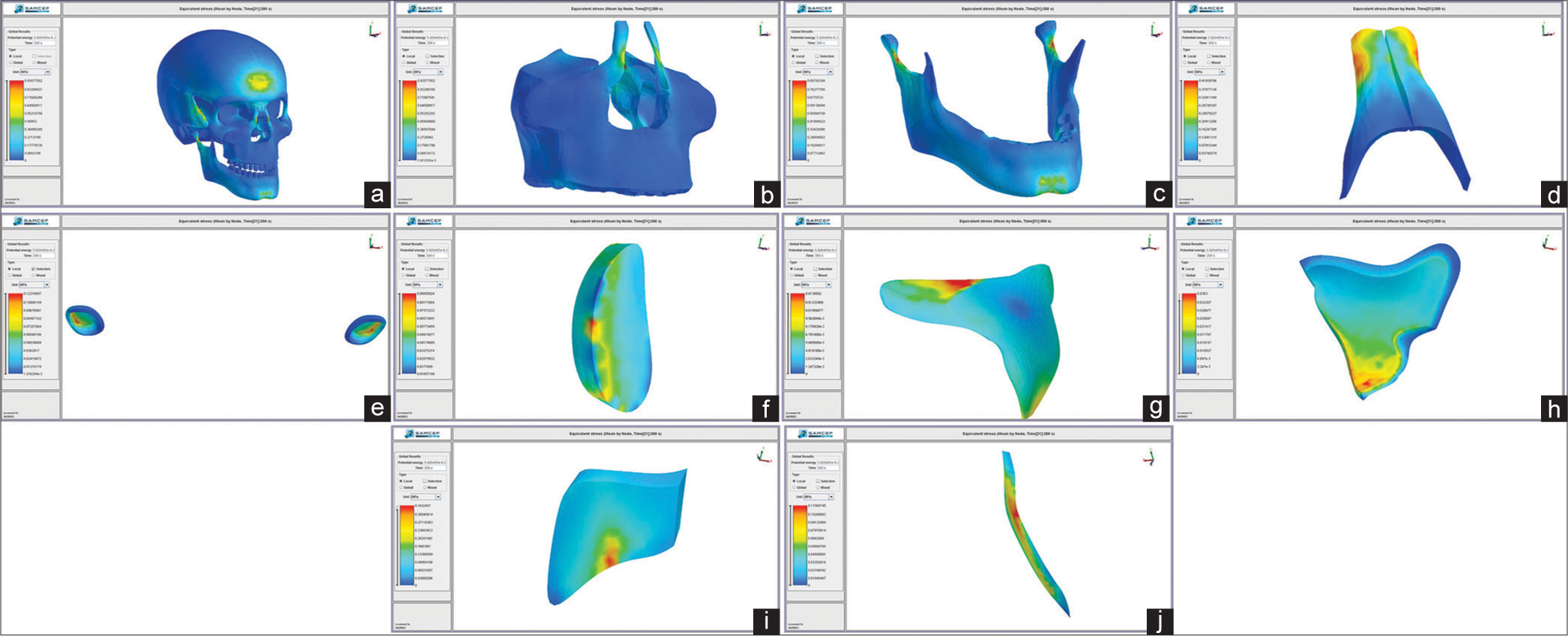
- (a) von Mises stress distribution on the craniofacial system in dental anchored face mask simulation, (b) von Mises stress distribution on the maxilla in dental anchored face mask simulation, (c) von Mises stress distribution on the mandible in dental anchored face mask simulation, (d) von Mises stress distribution on the nasal bone in dental anchored face mask simulation, (e) von Mises stress distribution on the temporomandibular joint discs in dental anchored face mask simulation, (f) von Mises stress distribution on the zygomaticotemporal suture in dental anchored face mask simulation, (g) von Mises stress distribution on the zygomaticomaxillary suture in dental anchored face mask simulation, (h) von Mises stress distribution on the pterygopalatine suture in dental anchored face mask simulation, (i) von Mises stress distribution on the frontomaxillary suture in dental anchored face mask simulation, (j) von Mises stress distribution on the nasomaxillary suture in dental anchored face mask simulation
In skeletal anchored face mask simulation, high von Mises stress values were seen in aperture piriform region (0.74 MPa), condyle necks (0.61 MPa), forehead (0.47 MPa), zygomatic bone (0.44 MPa), frontal edge of nasal bone (0.13 MPa), TMJ disc (0.08 MPa), zygomaticotemporal suture (0.04 MPa), zygomaticomaxillary suture (0.01 MPa), pterygopalatine suture (0.009 MPa), frontomaxillary suture (0.005 MPa), and nasomaxillary suture (0.002 MPa) in descending order [Figure 2a-j].

- (a) von Mises stress distribution on the craniofacial system in skeletal anchored face mask simulation, (b) von Mises stress distribution on the maxilla in skeletal anchored face mask simulation, (c) von Mises stress distribution on the mandible in skeletal anchored face mask simulation, (d) von Mises stress distribution on the nasal bone in skeletal anchored face mask simulation, (e) von Mises stress distribution on the temporomandibular joint discs in skeletal anchored face mask simulation, (f) von Mises stress distribution on the zygomaticotemporal suture in skeletal anchored face mask simulation, (g) von Mises stress distribution on the zygomaticomaxillary suture in skeletal anchored face mask simulation, (h) von Mises stress distribution on the pterygopalatine suture in skeletal anchored face mask simulation, (i) von Mises stress distribution on the frontomaxillary suture in skeletal anchored face mask simulation, (j) von Mises stress distribution on the nasomaxillary suture in skeletal anchored face mask simulation
In pterygopalatine and zygomaticomaxillary sutures, more uniform stress distributions were seen in skeletal anchored face mask [Figure 2g and h] than in dental anchored face mask [Figure 1g and h]. In zygomaticotemporal sutures, stress magnitudes were higher in skeletal anchored face mask [Figure 2f]. In zygomaticomaxillary sutures, stress magnitudes were similar and more uniform in skeletal anchored face mask [Figure 2h and j] when compared to stresses seen in dental anchored face mask [Figure 1h and j]. In pterygopalatine sutures, stress magnitudes in skeletal anchored face mask were lower and more uniform when compared to dental anchored face mask. In frontomaxillary sutures, stress distribution patterns were the same in both simulations; however, in skeletal anchored face mask simulation, stress magnitudes were slightly lower. In nasomaxillary sutures, more uniform stress distribution and lower stress magnitudes were observed in skeletal anchored face mask simulation compared to dental anchored face mask simulation [Figures 1i and 2i].
In dental anchored face mask simulation, higher von Mises stress magnitudes were seen in zygomaticotemporal, pterygopalatine, and zygomaticomaxillary sutures following nasomaxillary and frontomaxillary sutures [Figure 1f-j]. In skeletal anchored face mask simulation, higher stress magnitudes were seen in pterygopalatine, frontomaxillary, and nasomaxillary sutures following zygomaticotemporal and zygomaticomaxillary sutures [Figure 2f-j].
In TMJ discs, stresses were located on the lateroposterior part of the discs similarly in both simulations and von Mises stress values were higher in dental anchored face mask simulation [Figures 1e and 2e].
Stresses were located on the frontal edge of the nasal bone in skeletal anchored face mask simulation [Figure 2d], and in dental anchored face mask, stresses were located in a larger area on the frontal edge of the nasal bone in lower magnitude compared to skeletal anchored face mask simulation [Figure 1d].
On the mandible, von Mises stresses were located on the chin and condyle necks in both simulations; however, stress values were higher in dental anchored face mask simulation [Figures 1c and 2c].
In dental anchored face mask simulation, von Mises stresses were located in anterior borders of the frontal processes of the maxilla [Figure 1b], and in the skeletal anchored face mask simulation, stresses were located on the aperture piriform region where the protraction force was applied [Figure 2b]. On the anterior border of the frontal process of the maxilla, higher values of stresses were seen in dental anchored face mask simulation.
In dental anchored simulation, mild counterclockwise rotation was seen on the maxilla [Figure 3a and b]. However, in skeletal anchored face mask simulation, maxilla moved forward almost in a parallel pattern [Figure 4a and b].

- (a) Displacements in the craniofacial system in dental anchored face mask simulation, (b) displacements in the maxilla in dental anchored face mask simulation, (c) displacements in the mandible in dental anchored face mask simulation, (d) displacements in the temporomandibular joint discs in dental anchored face mask simulation

- (a) Displacements in the craniofacial system in skeletal anchored face mask simulation, (b) displacements in the maxilla in skeletal anchored face mask simulation, (c) displacements in the mandible in skeletal anchored face mask simulation, (d) displacements in the temporomandibular joint discs in skeletal anchored face mask simulation
Deformations on the TMJ discs, condyle heads, and mandible were higher in the dental anchored face mask simulation [Figures 3c and d] than in the skeletal anchored simulation [Figures 4c and d].
Discussion
FE analysis is a computational procedure to calculate the stress in an element, which performs a model solution. This structural analysis allows the determination of stress resulting from external force, pressure, thermal change, and other factors. This method is extremely useful for indicating mechanical aspects of biomaterials and human tissues that can hardly be measured in vivo.[17]
FE analysis is being used extensively in almost all the fields of dentistry and medicine. In orthodontics, it is used on complex tooth-periodontal models, the models of a part of the craniofacial system or orthodontic appliances, and temporary anchorage devices. The FE modeling of the craniofacial complex has been improved greatly in recent years. Miyasaka-Hiraga et al.[18] established a FE model of a skull consisting of 1776 individual elements in 1994. Holberg and Rudzki-Janson[19] established a FE model of a skull consisting of 53,555 tetrahedral, parametric single elements and 97,550 nodes in 2007. Boryor et al.[20] improved the FE model of the skull, which consisted of 2,403,023 tetrahedral elements and 514,224 nodes in 2008. In our study, 3D craniofacial model was consisted of 539,262 elements and 135,823 nodes to improve the precision.
In our study, in both simulations, maxillary counterclockwise rotation was seen with the force vector of 30°. Although rotation occurred in both simulations, in skeletal anchored simulation, maxilla almost made a parallel movement [Figures 3a, b and 4a, b]. This finding is in agreement with the findings of the study of Gautam et al.[21] in which they applied 1 kgf protraction force to the maxilla from the canine teeth in 30° relative to the occlusal plane and reported a counterclockwise rotation in the maxilla.
Yan et al.[22] simulated skeletal anchored maxillary protraction and reported clockwise rotation of the maxilla with the force vector of 30° relative to the occlusal plane. The reason that this finding is in contrary of our finding, is the difference in force application points. In the study of Yan et al.,[22] force was applied from the infrazygomatic buttress which causes the direction of the force pass far from the center of rotation of the maxilla.
Lee and Baek[23] applied miniplates on the infrazygomatic buttress and aperture piriform region and simulated skeletal maxillary protraction by the FE analysis. It was reported that with the force applied from the aperture pirifoms, maxilla moved forward and downward, and with the force applied from the infrazygomatic buttress, counterclockwise rotation on the maxilla was seen.
In both simulations in our study, uniform stresses were observed on the maxillary base, and stresses were mildly higher on the frontal process of the maxilla. The stresses seen in the frontal process were higher in the dental anchored face mask [Figures 1b and 2b]. The reason for this is thought to be the counterclockwise rotation of the maxilla around the sutura naso-fronto-maxillaries, as being higher in the dental anchored face mask simulation.[24]
Tanne et al.[25] and Miyasaka-Hiraga et al.[18] reported that the center of resistance of the nasomaxillary complex was on the posterosuperior edge of the pterygomaxillary fissure, and for the parallel movement of the nasomaxillary complex, maxillary protraction force should pass close to this point. The reason for the almost parallel movement of the maxilla in skeletal anchored face mask simulation in our study is thought to be that the force vector passed close to the center of resistance of the nasomaxillary complex.
Kircelli and Pektas[26] reported that applying the maxillary protraction force from the miniplates on the nasal walls caused the force directly to be transmitted on the bone and this application was a good treatment choice in the patients with skeletal Class III malocclusion. Moreover, they also supported that the force applied from the aperture piriforms would also pass through the center of the nasomaxillary complex and with this application, force would be more effective on the circummaxillary sutures. In our study, in skeletal anchored face mask simulation, the force direction passed close to the center of resistance by applying from the aperture piriforms and this inhibited the counterclockwise rotation of the maxilla as Kircelli and Pektas[26] suggested.
Stresses distributed in both simulations were higher on the lower edge of the chin and condyle necks. In the FE studies about maxillary protraction,[21,25,27-30] the force which was generated by the chin part of the face mask was ignored whereas the force transmitted to the TMJ by the chin part of the face mask is reported to be 70%–75% of the protraction force applied on the maxilla.[13] Yu et al.[31] evaluated the effects of maxillary protraction with and without rapid palatal expansion and reported that ignoring the force transmitted to the chin by the face mask was a lack of the study and they suggested that this point should be taken into account for the accuracy of further studies.
In our study, the force generated by the chin part of the face mask was also simulated and its effect on the craniofacial structures was evaluated. The stresses distributed on the condyle necks and the chin are a result of the force transmitted by the chin part of the face mask.
Yan et al.[22] evaluated the effects of the maxillary protraction force with 0°, 10°, 20°, and 30° force vectors relative to the occlusal plane with the skeletal and dental anchorage using the FE analysis. They applied the skeletal anchorage force from the infrazygomatic area and dental anchorage force from the first molar teeth. In the same force vector, higher stresses were observed in zygomaticomaxillary, zygomaticotemporal, and pterygopalatine sutures in the skeletal anchored simulation. In nasion and nasal wings area, higher stresses were observed in the dental anchored simulation. According to these findings, authors reported that stresses which induce the growth on the sutures posterior of the maxilla were generated by the skeletal anchorage and stresses which activate the osteogenesis in the nasal area were generated by the dental anchored face mask and authors suggested that this would affect the improvement of the profile. In accordance with this, Liu et al.[32] applied the miniplates on the aperture piriform regions and took the hooks out of the nostrils and applied the protraction force. Researchers reported that, with the sutural distraction osteogenesis, significant middle face improvement was achieved.
In the study of Lee and Baek,[23] stresses seen on the frontonasal, frontomaxillary, zygomaticomaxillary and pterygomaxillary sutures with the protraction from the miniplates applied on the aperture prifiorms were lower from the stresses seen in the protraction from the miniplates applied on the infrazygomatic buttress. Nonetheless, in accordance with the findings of Tanne and Sakuda[29] and Gautam et al.’s[30] studies, higher von Mises stresses were observed on the pterygomaxillary, zygomaticotemporal, zygomaticomaxillary, and frontonasal sutures in descending order. In our study, high von Mises stresses were seen in nasomaxillary, frontomaxillary, zygomaticotemporal, pterygopalatine, and zygomaticomaxillary sutures in descending order in dental anchored face mask [Figure 1a-j]. In skeletal anchored face mask simulation, high stresses were seen in zygomaticotemporal, zygomaticomaxillary, pterygopalatine, frontomaxillary, and nasomaxillary sutures in descending order [Figure 2a-j].
According to the functional matrix hypothesis of Moss,[33,34] a functional matrix consisting of cells that make up muscle, soft tissue, nerve, and so on might be a key determinant of facial growth. In this study, FE models simulated the force only from maxillary protraction, not from the soft tissues, such as muscles and skin. This is a limitation of FE approach. Reliability of the results is based on the modeling system. Hence, modeling is a crucial step when performing a FE study. Furthermore, results must be evaluated with great care.
Conclusions
In our study, craniofacial structures were 3D modeled and protraction force of 750 g per side directed from the upper canines in the first simulation and the same force vector directed from the maxillary bone on aperture piriform regions were applied forward and 30° downward relative to the occlusal plane. Comparing both simulations, maxilla moved in a more parallel pattern in skeletal anchored model. This type of movement is often desired by clinicians. By varying the anchorage method, location, and force vector, orthodontists can alter the magnitude of the movement of maxilla due to the cases’ needs.
FE analysis is a reliable numerical method that is easy and cost-effective. It is useful for problems with complicated geometries, loadings and material properties such as craniofacial complex. Thus, we used this analysis method in our study to determine the stress values when external forces are applied to the craniofacial complex. Considering the limitations, further new ideas can be easily implied using FE method.
Financial support and sponsorship
We would like to thank TÜBİTAK (the scientific and technological research council of Turkey, Project Number: 13770).
Conflicts of interest
There are no conflicts of interest.
References
- Clinical results of the maxillary protraction in Korean children. Am J Orthod Dentofacial Orthop. 1995;108:583-92.
- [CrossRef] [Google Scholar]
- Maxillary protraction: Treatment and posttreatment effects. Am J Orthod Dentofacial Orthop. 1998;113:612-9.
- [CrossRef] [Google Scholar]
- Orthodontic and orthopaedic changes associated with treatment in subjects with class III malocclusions. Eur J Orthod. 2006;28:496-502.
- [CrossRef] [PubMed] [Google Scholar]
- The effectiveness of protraction face mask therapy: A meta-analysis. Am J Orthod Dentofacial Orthop. 1999;115:675-85.
- [Google Scholar]
- Assessment of skeletal and dental changes by maxillary protraction. Am J Orthod Dentofacial Orthop. 1998;114:492-502.
- [Google Scholar]
- Long-term follow-up of early treatment with reverse headgear. Eur J Orthod. 2003;25:95-102.
- [Google Scholar]
- Long-term efficacy of reverse pull headgear therapy. Angle Orthod. 2006;76:915-22.
- [CrossRef] [PubMed] [Google Scholar]
- Dentofacial effects of bone-anchored maxillary protraction: A controlled study of consecutively treated class III patients. Am J Orthod Dentofacial Orthop. 2010;138:577-81.
- [Google Scholar]
- Comparison of two protocols for maxillary protraction: Bone anchors versus face mask with rapid maxillary expansion. Angle Orthod. 2010;80:799-806.
- [CrossRef] [PubMed] [Google Scholar]
- Three-dimensional analysis of maxillary protraction with intermaxillary elastics to miniplates. Am J Orthod Dentofacial Orthop. 2010;137:274-84.
- [Google Scholar]
- Orthopedic protraction with skeletal anchorage in a patient with maxillary hypoplasia and hypodontia. Angle Orthod. 2006;76:156-63.
- [Google Scholar]
- The efficacy of maxillary protraction protocols with the micro-implant-assisted rapid palatal expander (MARPE) and the novel N2 mini-implant-a finite element study. Prog Orthod. 2015;16:16.
- [Google Scholar]
- A mathematical model for the computation of the forces exerted by the facial orthopedic mask. Am J Orthod Dentofacial Orthop. 1992;101:441-8.
- [Google Scholar]
- Stress distribution in the temporomandibular joint after mandibular protraction: A 3-dimensional finite element method study. Part 1. Am J Orthod Dentofacial Orthop. 2009;135:737-48.
- [Google Scholar]
- Association between mechanical stress and bone remodeling. J Osaka Univ Dent Sch. 1990;30:64-71.
- [Google Scholar]
- Three-dimensional finite-element model of the human temporomandibular joint disc during prolonged clenching. Eur J Oral Sci. 2006;114:441-8.
- [Google Scholar]
- Revolution in orthodontics: Finite element analysis. J Int Soc Prev Community Dent. 2016;6:110-4.
- [CrossRef] [PubMed] [Google Scholar]
- Finite element analysis for stresses in the craniofacial sutures produced by maxillary protraction forces applied at the upper canines. Br J Orthod. 1994;21:343-8.
- [CrossRef] [Google Scholar]
- Stresses at the cranial base induced by rapid maxillary expansion. Angle Orthod. 2006;76:543-50.
- [Google Scholar]
- Stress distribution and displacement analysis during an intermaxillary disjunction – A three-dimensional FEM study of a human skull. J Biomech. 2008;41:376-82.
- [Google Scholar]
- Skeletal response to maxillary protraction with and without maxillary expansion: A finite element study. Am J Orthod Dentofacial Orthop. 2009;135:723-8.
- [Google Scholar]
- Three-dimensional finite element analysis of the craniomaxillary complex during maxillary protraction with bone anchorage vs conventional dental anchorage. Am J Orthod Dentofacial Orthop. 2013;143:197-205.
- [Google Scholar]
- Stress and displacement between maxillary protraction with miniplates placed at the infrazygomatic crest and the lateral nasal wall: A 3-dimensional finite element analysis. Am J Orthod Dentofacial Orthop. 2012;141:345-51.
- [Google Scholar]
- Effects of directions of maxillary protraction forces on biomechanical changes in craniofacial complex. Eur J Orthod. 1989;11:382-91.
- [CrossRef] [PubMed] [Google Scholar]
- Midfacial protraction with skeletally anchored face mask therapy: A novel approach and preliminary results. Am J Orthod Dentofacial Orthop. 2008;133:440-9.
- [Google Scholar]
- Changes in orthodontic cephalometric reference points on application of orthopedic force to jaw: Three-dimensional finite element analysis. Bull Tokyo Dent Coll. 2005;46:59-65.
- [CrossRef] [PubMed] [Google Scholar]
- Biomechanical effect of anteriorly directed extraoral forces on the craniofacial complex: A study using the finite element method. Am J Orthod Dentofacial Orthop. 1989;95:200-7.
- [Google Scholar]
- Biomechanical and clinical changes of the craniofacial complex from orthopedic maxillary protraction. Angle Orthod. 1991;61:145-52.
- [Google Scholar]
- Maxillary protraction with and without maxillary expansion: A finite element analysis of sutural stresses. Am J Orthod Dentofacial Orthop. 2009;136:361-6.
- [Google Scholar]
- Three-dimensional finite-element analysis of maxillary protraction with and without rapid palatal expansion. Eur J Orthod. 2007;29:118-25.
- [CrossRef] [PubMed] [Google Scholar]
- Sutural distraction osteogenesis (SDO) versus osteotomy distraction osteogenesis (ODO) for midfacial advancement: A new technique and primary clinical report. J Craniofac Surg. 2005;16:537-48.
- [Google Scholar]
- The functional matrix hypothesis revisited 1. The role of mechanotransduction. Am J Orthod Dentofacial Orthop. 1997;112:8-11.
- [Google Scholar]
- The functional matrix hypothesis revisited 2. The role of an osseous connected cellular network. Am J Orthod Dentofacial Orthop. 1997;112:221-6.
- [CrossRef] [Google Scholar]






